I. Giới thiệu chung về số nghiệm của phương trình
Trong toán học, việc tìm hiểu về số nghiệm của phương trình là một trong những kỹ năng quan trọng nhất. Không chỉ giúp giải quyết các bài toán cụ thể, nó còn phát triển tư duy logic và khả năng phân tích vấn đề.

II. Các loại phương trình và số nghiệm tương ứng
1. Phương trình bậc nhất (ax + b = 0)
- Có duy nhất một nghiệm khi a ≠ 0: x = -b/a
- Vô nghiệm khi a = 0 và b ≠ 0
- Vô số nghiệm khi a = b = 0
2. Phương trình bậc hai (ax² + bx + c = 0)
- Dựa vào định thức Δ = b² – 4ac:
- Δ > 0: có hai nghiệm phân biệt
- Δ = 0: có nghiệm kép
- Δ < 0: vô nghiệm trong tập số thực
3. Phương trình bậc ba (ax³ + bx² + cx + d = 0)
- Luôn có ít nhất một nghiệm thực
- Có thể có 1, 2 hoặc 3 nghiệm thực
- Phương pháp giải:
- Phương pháp Cardano
- Phân tích thành nhân tử
- Tìm nghiệm hữu tỉ
III. Phương pháp xác định số nghiệm
1. Phương pháp đại số
- Biến đổi tương đương
- Phân tích thành nhân tử
- Áp dụng công thức nghiệm
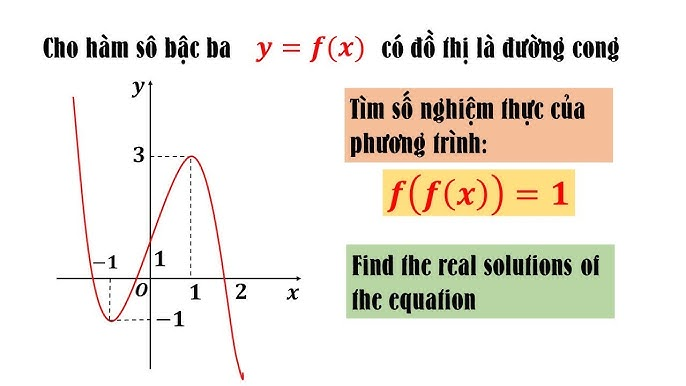
2. Phương pháp đồ thị
- Số giao điểm của đồ thị với trục hoành
- Số giao điểm của hai đồ thị
- Phân tích tính đơn điệu
3. Phương pháp sử dụng các định lý
- Định lý Viet
- Định lý về dấu của hàm số
- Định lý về tính liên tục
IV. Các dạng bài tập thường gặp
1. Bài tập về tham số
Ví dụ: Tìm điều kiện của m để phương trình (m+1)x² + 2mx + 1 = 0 có hai nghiệm phân biệt.
Lời giải:
1) Đặt a = m+1, b = 2m, c = 1
2) Để có hai nghiệm phân biệt: Δ > 0
3) Δ = 4m² – 4(m+1)(1) > 0
4) Δ = 4m² – 4m – 4 > 0
5) m² – m – 1 > 0
6) m < (-1-√5)/2 hoặc m > (-1+√5)/2
2. Bài tập về quan hệ giữa các nghiệm
Ví dụ: Chứng minh tổng bình phương hai nghiệm của phương trình x² + px + q = 0 bằng p² – 2q.
Lời giải:
1) Gọi x₁, x₂ là hai nghiệm
2) Theo Viet: x₁ + x₂ = -p và x₁x₂ = q
3) (x₁ + x₂)² = p²
4) 2x₁x₂ = 2q
5) x₁² + x₂² = (x₁ + x₂)² – 2x₁x₂ = p² – 2q
V. Mẹo và kỹ thuật giải nhanh
1. Nhận biết nhanh số nghiệm
- Dựa vào hệ số
- Dựa vào dấu các giá trị đặc biệt
- Dựa vào tính chất đối xứng
2. Các công thức đặc biệt
- Công thức nghiệm bậc hai
- Công thức nghiệm trùng
- Công thức Viet mở rộng
VI. Ứng dụng trong thực tế
1. Trong vật lý
- Bài toán chuyển động
- Bài toán điện học
- Bài toán nhiệt học
2. Trong kinh tế
- Bài toán tối ưu
- Bài toán lãi suất
- Bài toán chi phí-lợi nhuận
VII. Lời khuyên cho học sinh
- Nắm vững lý thuyết cơ bản
- Luyện tập nhiều dạng bài tập khác nhau
- Phân tích kỹ yêu cầu đề bài
- Kiểm tra lại kết quả
VIII. Kết luận
Việc hiểu rõ về số nghiệm của phương trình không chỉ giúp học sinh giải quyết tốt các bài toán trong chương trình học mà còn phát triển tư duy logic và khả năng giải quyết vấn đề. Đây là kiến thức nền tảng quan trọng cho nhiều môn học khác và các ứng dụng thực tế.
Để được tư vấn và hỗ trợ thêm về môn Toán cũng như các môn học khác, vui lòng liên hệ:
Cánh Học Tiếng Anh
- Hotline: 0909 333 000
- Email: [email protected]
- Website: https://cachhoctienganh.net
Cánh Học Tiếng Anh tự hào là đơn vị tiên phong trong việc cung cấp các phương pháp học tập hiệu quả, với đội ngũ giáo viên giàu kinh nghiệm và tận tâm. Chúng tôi không chỉ giúp học sinh nâng cao kiến thức mà còn phát triển kỹ năng tư duy và phương pháp học tập khoa học.


